Diagramma di Bode

uni
Un diagramma di Bode è una rappresentazione grafica della Risposta in Frequenza di un Sistema LTI e che consiste in due grafici che rappresentano rispettivamente l’ampiezza (o modulo) e la fase della funzione complessa di risposta in frequenza.
Questo diagramma può anche essere usato su sistemi instabili, dei quali quindi non ha senso studiare una risposta in frequenza.

• il modulo $|G(jw)|$ viene espresso in deciBel: $|G(jw){|}_{dB}=20{\log }_{10}(|G(jw)|$.
• la fase viene espressa linearmente, in gradi o in radianti.
• per la pulsazione viene usata una scala logaritmica invece, quindi una unità equivale ad un fattore 10
• Una unità sull’ascissa prende il nome di decade: ovvero la distanza in scala logaritmica tra due numeri cui rapporto è 10.
• Ottava è invece la distanza in scala logaritmica tra due numeri cui rapporto è 2.

È importante osservare che per le proprietà logaritmo del prodotto e della proprietà di Convoluzione della Trasformata di Laplace, se volessi trovare il diagramma di Bode di due sistemi collegati in serie, basta sommare i grafici dei due sistemi.

Rappresentazione di una FdT tramite il diagramma di Bode

Porto la Funzione di Trasferimento in Forma di Bode:

$$G(jw)=\frac{\stackrel{\text{Guadagno di Bode}}{\overbrace{K_B}}}{\underset{\text{Poli nell’origine}}{\underbrace{(jw{)}^h}}}\frac{{\prod }_{i=1}^{m-n}(\stackrel{\text{zeri semplici}}{\overbrace{1\pm jw{T}_{zi}}})}{{\prod }_{i=1}^{n-h-r}(\underset{\text{Poli semplici}}{\underbrace{1\pm jw{T}_{pi}}})}\frac{{\prod }_{i=1}^n(\stackrel{\text{zeri complessi coniugati}}{\overbrace{1\pm jw\frac{2{\xi }_{zi}}{w_{0zi}}-\frac{w^2}{w_{0zi}^2}}})}{{\prod }_{i=1}^r(\underset{\text{Poli complessi coniugati}}{\underbrace{1\pm jw\frac{2{\xi }_{pi}}{w_{0pi}}-\frac{w^2}{w_{0pi}^2}}})}$$

Costruisco ora il diagramma di Bode come somma delle singole Funzioni Elementari.

Valori Comuni di Guadagno in Decibel

$G(0)$	$\Vert G(0){\Vert }_{dB}$
1	0
2	6
3	9.5
5	14
6	15.5
7	17
8	18
9	19
10	20

Margini di Fase e di Guadagno

Dall’osservazione del diagramma di Bode è possibile osservare la stabilità del sistema.

==L’osservazione di questi margini ha senso solo se il sistema è stabile in catena aperta, e solo se il sistema è Regolare¹.==

1. Margine di Guadagno: $m_G=0-|G(s_0){|}_{dB}$ con $s:\varphi G(s_0)=-180\mathrm{deg}$. Ovvero il margine di guadagno è quanto sotto a $0dB$ è il modulo quando la fase tocca i $180$ gradi.
   Un sistema in catena aperta è stabile in catena chiusa se $m_G>0dB$
2. Margine di Fase: $m_{\varphi }=180+\varphi G(s_0)$ con $s_0:|G(s_0)|=0dB$. Ovvero il margine di fase è quanto sopra a $-180$ gradi è la fase quando il modulo tocca i $0dB$.
   Un sistema in catena aperta è stabile in catena chiusa se $m_{\varphi }>0\mathrm{deg}$

Essenzialmente quello che facciamo quando valutiamo questi margini è valutare la distanza del nostro sistema in catena aperta dal punto $-1$, perché il sistema in catena chiusa è $G_{cl}(s)=\frac{G(s)}{1+G(s)}$ e dobbiamo quindi evitare che il nostro denominatore vada a $0$.

Sono considerati “buoni” margini i seguenti valori:

• $m_G>4dB/6dB$
• $m_{\varphi }>35deg$

Se i margini di fase e di guadagno non esistono possiamo avere questi due casi:

• $|G(s)|dB>0dB\forall w$: il sistema è potenzialmente instabile e non puoi garantire la stabilità in ciclo chiuso
• $|G(s)|dB<0dB\forall w$: il sistema è stabile, ma lento. Il sistema in ciclo chiuso è molto robusto ma lento. Sistema probabilmente sovraconservativo.

Esempio di Sistema Stabile in Catena chiusa:

Funzioni Elementari

Guadagno Costante

$$\begin{array}{c}G(s)=k\\ G(jw)=|k|e^{j\varphi }\\ |G(jw)|=|k|\\ \varphi G=\{\begin{array}{ll}0& k>0\\ -\pi & k<0\end{array}\end{array}$$

Polo nell’Origine

$$\begin{array}{c}G(s)=\frac{1}{s}\\ G(jw)=\frac{1}{jw}\\ |G(jw)|=\frac{1}{w}\\ \varphi G=-\frac{\pi }{2}\end{array}$$

Polo Semplice

$$\begin{array}{c}G(s)=\frac{1}{1+\tau s}\\ G(jw)=\frac{1}{1+\tau jw}\\ |G(jw)|=\frac{1}{\sqrt{1+{\tau }^2{w}^2}}\\ \varphi G=-\arctan (\tau w)\end{array}$$

Zero Semplice

$$\begin{array}{c}G(s)=1+\tau s\\ G(jw)=1+\tau jw\\ |G(jw)|=\sqrt{1+{\tau }^2{w}^2}\\ \varphi G=\arctan (\tau w)\end{array}$$

Polo Complesso

$$\begin{array}{cc}G(s)=\frac{1}{1+\frac{2\xi }{w_0}s+\frac{s^2}{w_0^2}}& \\ G(jw)=\frac{1}{1+\frac{2\xi }{w_0}jw-\frac{w^2}{w_0^2}}& \\ |G(jw)|=\frac{1}{\sqrt{{\left(1-\frac{w^2}{w_0^2}\right)}^2+4\frac{w^2}{w_0^2}{\xi }^2}}& \{\begin{array}{ll}|G(jw){|}_{dB}=0& w<<w_0\\ |G(jw){|}_{dB}=40\log (w_0)-40\log (w)& w>>w_0\\ |G(jw){|}_{dB}=\frac{1}{2\xi }& w=w_0\end{array}\\ \varphi G(jw)=atan2\left(\frac{2\xi w{w}_0}{w_0^2-w^2}\right)& \{\begin{array}{ll}\varphi G(jw)=0& w<<w_0\\ \varphi G(jw)=-\frac{\pi }{2}& w=w_0\\ \varphi G(jw)=-\pi & w>>w_0\end{array}\end{array}$$

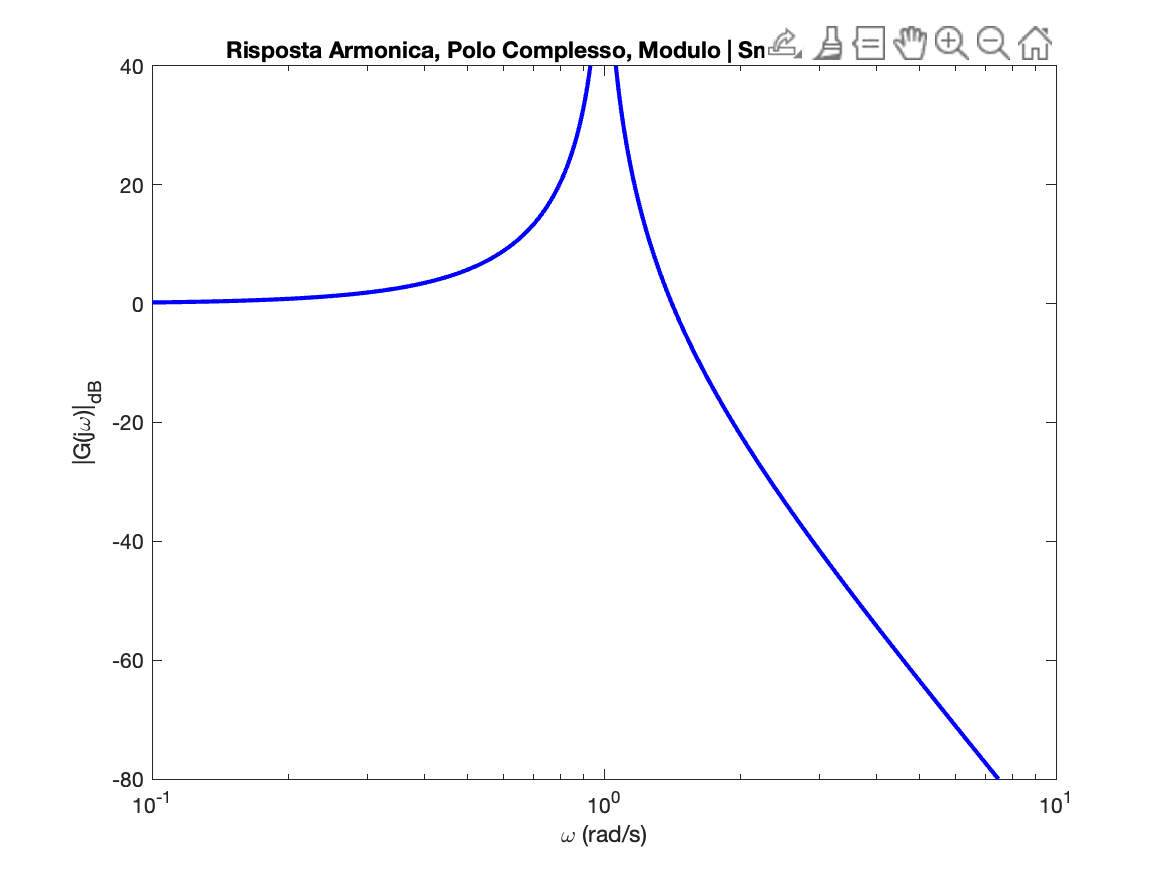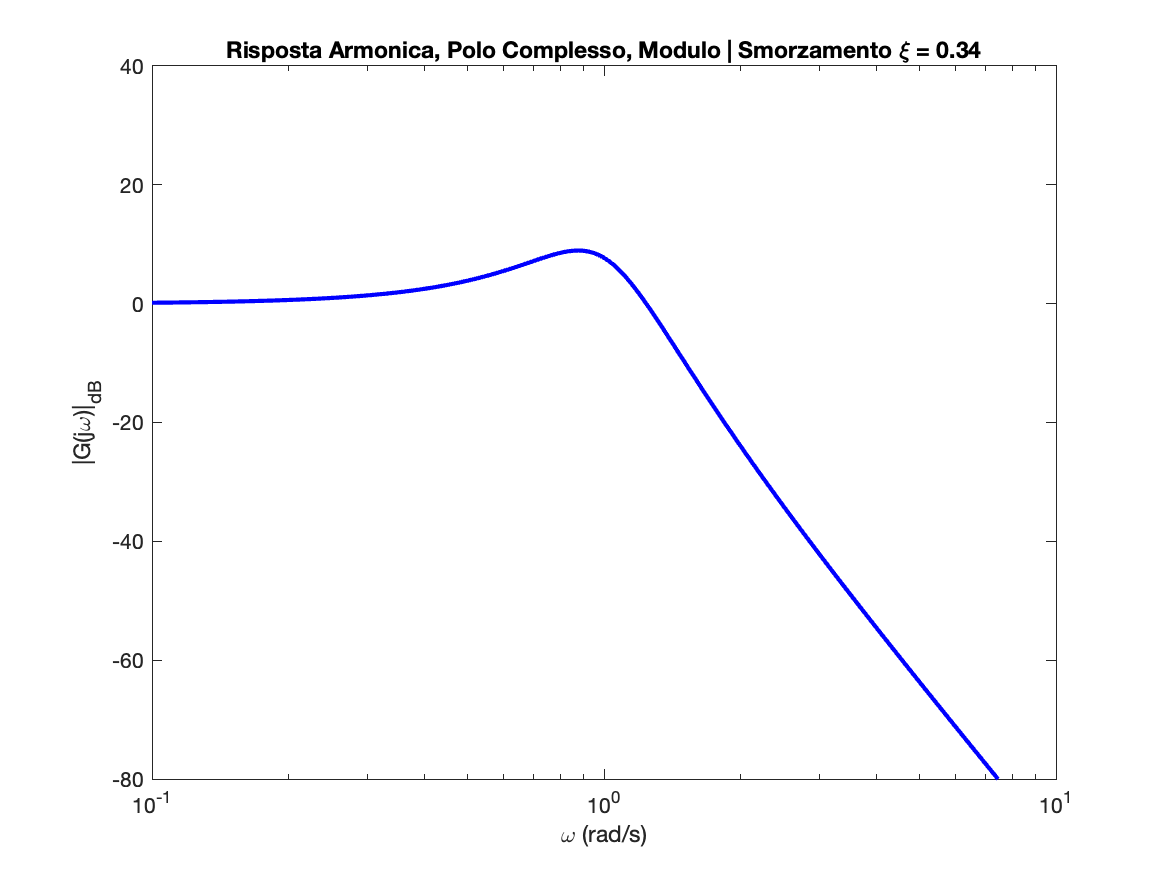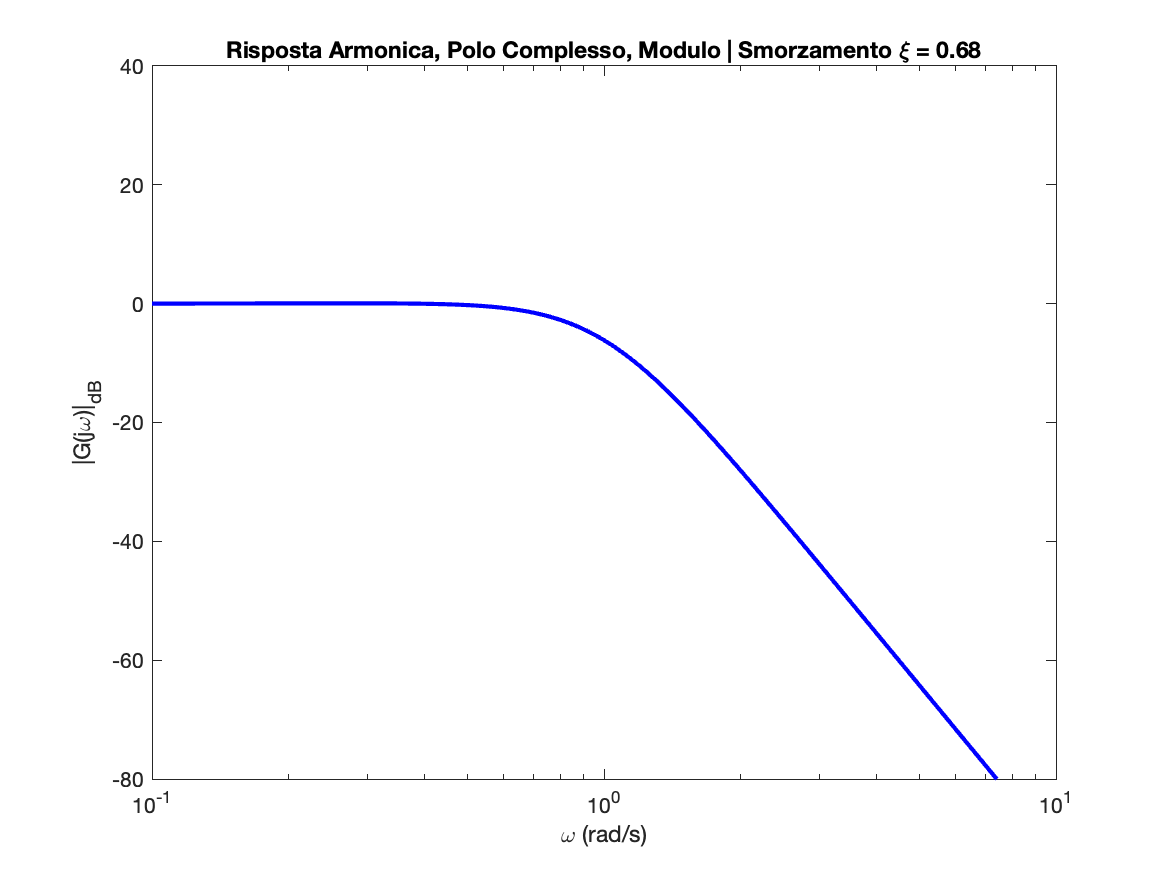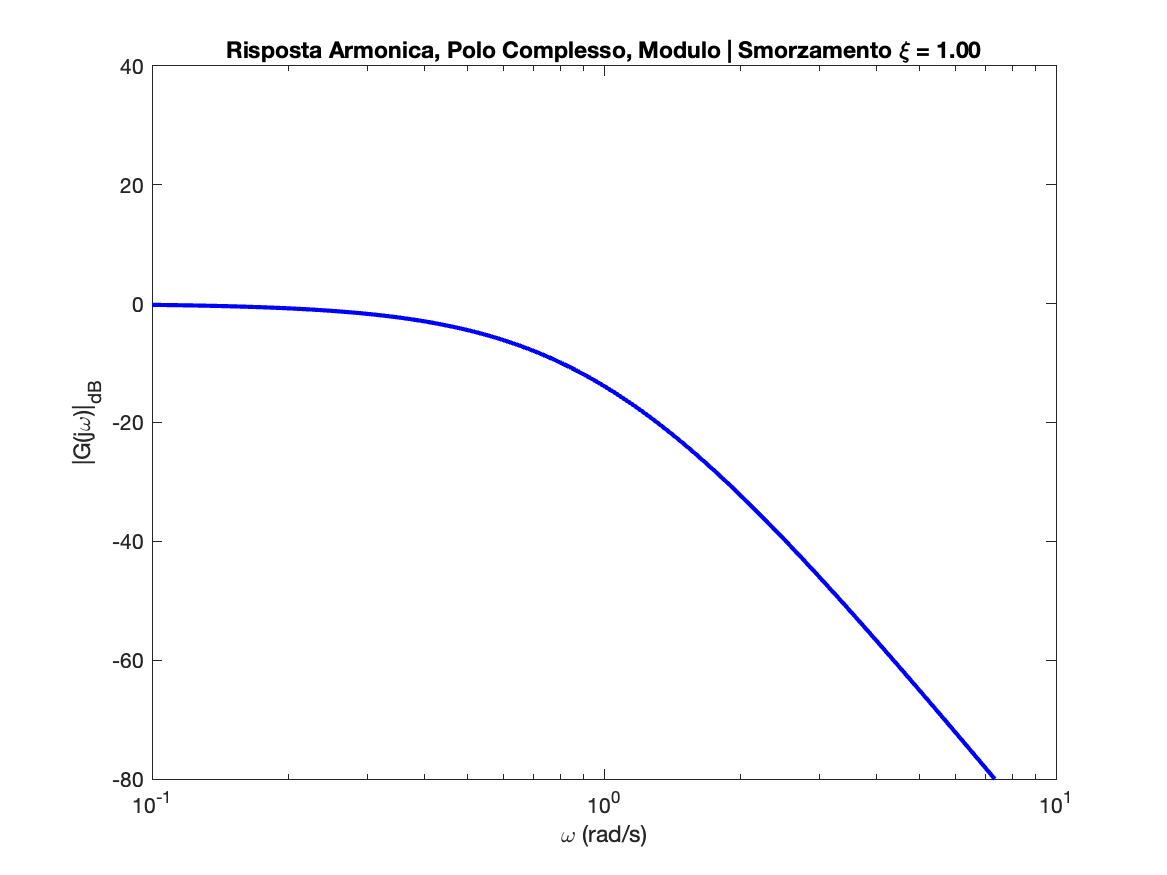
Zero Complesso

Ritardo Puro

$$\begin{array}{c}G(s)=e^{-\tau s}\to G(jw)=e^{-\tau jw}\\ |G(jw)|=1\to |G(jw){|}_{dB}=0\\ \varphi G=-w\tau \end{array}$$

Tabella Riassuntiva

	Modulo	punto di rottura		Fase	inclinazione	intervallo
Guadagno Statico $K$	$20\log (\Vert K\Vert )$	---		$0\text{ se }K\ge 0$ $-\pi \text{ se }K<0$	---	---
Zero in Origine	$+20dB/dec$	---		$+\frac{\pi }{2}$	---	---
Polo in Origine	$-20dB/dec$	---		$-\frac{\pi }{2}$	---	---
Zero Semplice	$+20dB/dec$	$\frac{1}{\tau }$		da $0$ a $\frac{\pi }{2}$	$\frac{\pi }{4}/dec$	$[\frac{1}{10\tau };\frac{10}{\tau }]$
Polo Semplice	$-20dB/dec$	$\frac{1}{\tau }$		da $0$ a $-\frac{\pi }{2}$	$-\frac{\pi }{4}/dec$	$[\frac{1}{10\tau };\frac{10}{\tau }]$
Zero Complesso	$-40\log (w_0)+40dB/dec$	$w_0$		da $0$ a $\pi$	$\frac{\pi }{2}/dec$	$[\frac{1}{10\tau };\frac{10}{\tau }]$
Polo Complesso	$40\log (w_0)-40dB/dec$	$w_0$		da $0$ a $-\pi$	$-\frac{\pi }{2}/dec$	$[\frac{1}{10\tau };\frac{10}{\tau }]$
Ritardo Puro	---	---				---

Footnotes

1. Un sistema in retroazione è regolare se l’ampiezza della FdT a ciclo aperto è funzione monotona decrescente della pulsazione. ↩