Numeri Immaginari (o Complessi)

uni

$$i=\sqrt{-1}$$ $$C=\{z=a+ib;a,b\in R\}$$

Piano di Gauss (Argand-Gauss)

Il piano di Gauss rappresenta su un piano cartesiano un numero complesso, mettendo sull’asse dell’ascissa la parte reale di $z$ e sull’ordinata il coefficiente della parte immaginaria di $z$.

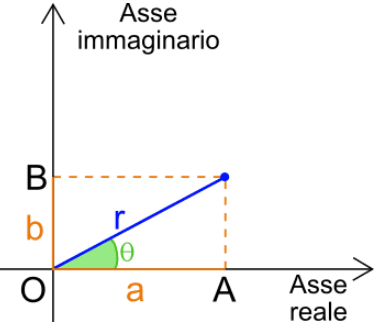
Forma Algebrica

$$z=a+ib$$

Con $a$: parte reale di $z$, e $b$: coefficiente della parte immaginaria di $z$, con $a,b\in R$

Somma

La somma si svolge semplicemente sommando parti reali e coefficienti tra di loro

Moltiplicazione

$$z_1\cdot z_2=(a_1{a}_2-b_1{b}_2)+i(a_1{b}_2+b_1{a}_2)$$

Forma Trigonometrica (o Polare)

$$z=r[cos(\theta )+isin(\theta )]$$

Con:
$r\ge 0$ e $r\in R$
$-\pi <\theta \le \pi$ oppure $0\le \theta <2\pi$
Dove $\theta$ è l’angolo compreso tra il segmento che porta a $z$ e l’asse reale, nel Piano di Gauss e $r$ è la lunghezza del segmento. Ne risulta che:
$a=r\cdot cos(\theta )$
$b=r\cdot sin(\theta )$
$z=r[cos(\theta )+isin(\theta )]$
$r$ è detto norma o modulo di $z$ e $\theta$ è detto argomento o anomalia di $z$.
La condizione $-\pi <\theta \le \pi$ oppure $0\le \theta <2\pi$ viene posto perché $sin$ e $cos$ son funzioni periodiche e la corrispondenza tra forma algebrica e polare di $z$ non sarebbe biunivoca. Un altro accorgimento affinché la corrispondenza sia biunivoca è porre il numero complesso $z=0$ come $r=0;\nexists \theta$

Coniugato Complesso

Il coniugato di un numero complesso $z$, indicato con $\overline{z}$, $z^{\ast }$ o $conj(z)$ è per definizione un numero complesso con parte reale uguale a $z$ e parte immaginaria uguale ma di segno opposto a $z$.
Quindi se $z=a+ib$ allora $\overline{z}=a-ib$.
Quindi se $z=r[cos(\theta )+isin(\theta )]$ allora $\overline{z}=r[cos(\theta )-isin(\theta )]$ oppure $\overline{z}=r[cos(-\theta )isin(-\theta )]$.
Quindi se $z=r{e}^{i\theta }$ allora $\overline{z}=r{e}^{-i\theta }$.

Inverso di un numero complesso

$z\cdot z^{-1}=1$
$z^{-1}=\frac{\overline{z}}{|z{|}^2}$ quindi se $z=a+ib$ allora $z^{-1}=\frac{a-ib}{a^2+b^2}$

Operazioni

Passaggio da Forma Algebrica a Forma Trigonometrica

$$r=\sqrt{a^2+b^2}$$

Per $\theta \in (-\pi ,\pi ]$ :

$$\theta =\{\begin{array}{l}\frac{\pi }{2}sea=0,b>0\\ -\frac{\pi }{2}sea=0,b<0\\ nondefinitosea=o,b=0\\ arctan(\frac{b}{a})sea>0,bqualsiasi\\ arctan(\frac{b}{a})+\pi sea<0,b\ge 0\\ arctan(\frac{b}{a})-\pi sea<0,b<o\end{array}$$

Per $\theta \in [0,2\pi )$ :

$$\theta =\{\begin{array}{l}\frac{\pi }{2}sea=0,b>0\\ \frac{3\pi }{2}sea=0,b<0\\ nondefinitosea=o,b=0\\ arctan(\frac{b}{a})+\pi sea<0,bqualsiasi\\ arctan(\frac{b}{a})+2\pi sea>0,b<0\\ arctan(\frac{b}{a})sea>0,b\ge 0\end{array}$$

Radice di un numero complesso

Ogni numero complesso ammette esattamente $n$ radici complesse n-esime, calcolate a partire dalla forma trigonometrica del numero complesso.

$$\sqrt[n]{z}=\sqrt[n]{r}\left(cos\right(\frac{\theta +2k\pi }{n})+isin(\frac{\theta +2kn}{n})$$

Dove $k$ è un numero naturale che varia tra $\{0,1,2,...(n-1)\}$. Al variare di $k$ la formula descrive tutte le $n$ radici n-esime di $z$. $\left(\frac{\theta }{n}\right)$ è detto argomento principale o anomalia principale delle radici.